waiting-queues

#area/zhaw/dps/theory

Waiting queues

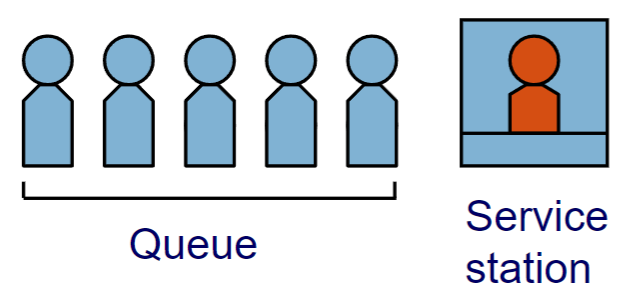
Pasted image 20230926154158.png

Parameters and characteristics

Waiting queues are described using a special notation: a/b/c
a: Probability distribution of arrival rate

D: Deterministic
M: Poisson
G: General

b: Probability distribution of service time

D: Deterministic
M: Exponential
G: General

c: Number of servers

All waiting queues run under these assumptions:

No restriction of the waiting room
Prioritization of customers is FCFS (first-come-first-serve)

Queue	Characteristics
`M/M/1`	Poisson-distributed arrivals often realistic
	Exponentially distributed handling times often out of touch with reality
	Very nice analytical properties: E.g. distribution of output is Poisson
	Very simple formulas for key performance indicators
`M/M/c`	Like M/M/1 with more than one server
	Formulas for key performance indicators more complex than for M/M/1
`M/G/1`	Often more realistic than M/M/1, since distribution of handling times arbitrarily
	Distribution of output not Poisson
	Simple formulas available for some KPIs
`G/G/c`	Very realistic modeling possible
	Calculation of performance, if possible, very complex

Modeling M/M/1 queues

For M/M/1 queues there are analytical properties available. These can be modeled via a probability model.

$A$ : Average interarrival time ( $0.5 hours/customer$ )
$λ$ : Arrival rate ( $2 customers/hour$ )

A = \frac{1}{λ} λ = \frac{1}{A}

$S$ : Average service time ( $0.25 hours/customer$ )
$μ$ : Service rate ( $4 customers/hour$ )

S = \frac{1}{μ} μ = \frac{1}{S}

$ρ$ : Utilization factor ( $50 %$ ), expected number of customers

ρ = \frac{λ}{μ}

$n$ : Number of customers in the system (queue + service)
$P_{n}$ : Probability that there are $n$ customers in the system at any given time

P_{n} = ρ^{n} (1 - ρ)

$L S$ : length system, expected number of customers in the system
$L Q$ : Length queue, expected number of customers in the queue

\begin{matrix} L S = \frac{ρ}{1 - ρ} L Q = \frac{ρ^{2}}{1 - ρ} \end{matrix}

$W S$ : expected time of a customer in the system
$W Q$ : Waiting time queue, expected time of a customer in the queue

\begin{matrix} W S = \frac{ρ}{λ (1 - ρ)} W Q = \frac{ρ^{2}}{λ (1 - ρ)} \end{matrix}

Modelling M/M/1 networks

A waiting queue network combines multiple waiting queues together.

$L S$ , $L Q$ : Are in all cases trivial the sum of the queues

\begin{matrix} L S = \sum_{i} L S_{i} L Q = \sum_{i} L Q_{i} \end{matrix}

$W S$ , $W Q$ : Need to take into account the relative probability if any.

\begin{matrix} W S = \sum_{i} p_{i} \cdot W S_{i} W Q = \sum_{i} p_{i} \cdot W Q_{i} \end{matrix}

Sequential

Pasted image 20231003104842.png
Due to the poisson distribution ( $λ_{i + 1} = λ_{i}$ ) $λ$ stays equal to all linked queues.

$W S$ , $L S$ : Is equal to the sum of all $W S$ and $L S$ respecivley.

\begin{matrix} W S = \sum_{i} W S_{i} L S = \sum_{i} L S_{i} \end{matrix}

Separation

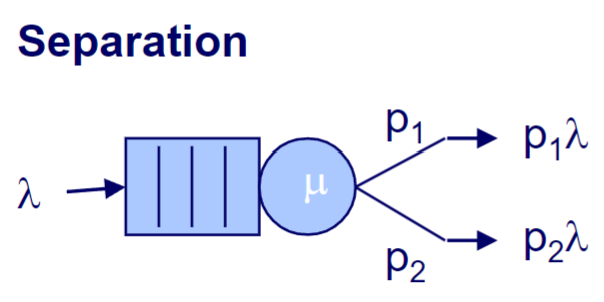
Pasted image 20231003105536.png

$p_{1}$ , $p_{2}$ : The probabilities going into one of the branches
$p_{1} λ$ , $p_{2} λ$ : The arrival rate for the different branches

Integration

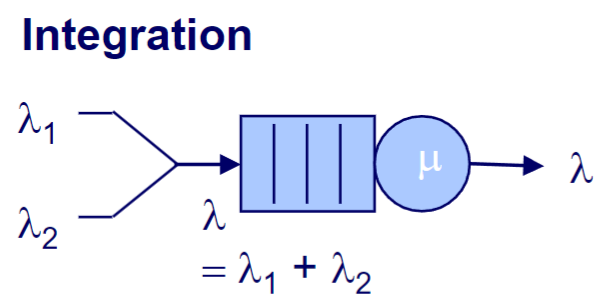
Pasted image 20231003105552.png

$λ_{1}$ , $λ_{2}$ : The arrival rate from the different branches
$λ$ : Is defined by the combined arrival rate

λ = λ_{1} + λ_{2}

Recursion

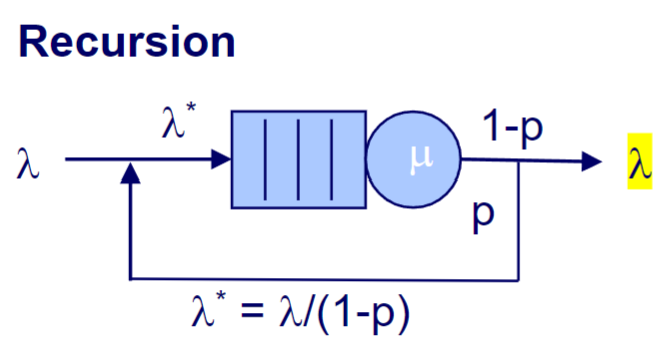
Pasted image 20231003105609.png

$p$ , $1 - p$ : The probability of doing a recursion
$λ^{*}$ : The arrival rate with the recursion taken into account

λ^{*} = \frac{λ}{1 - p}